이진 트리(Binary Tree)는 트리 구조의 가장 기본적이고, 기초적인 모델로 간주된다.
특히 컴퓨터 과학에서 트리 구조를 처음 배울 때 이진 트리를 가장 먼저 다루는 이유는 대략 다음과 같다:
- 이진 트리는 각 노드가 최대 두 개의 자식만을 가질 수 있기 때문에 구조적으로 간단하다.
- 여러 트리 구조가 이진 트리로부터 파생되었기 때문에(ex: 이진 탐색 트리, 균형 이진 트리 등), 이들을 이해하기 위해 이진 트리에 대한 이해가 선행되어야 한다.
그러므로 이진 트리를 이해하는 시간을 갖고, 이진 트리를 활용하여 트리의 노드를 스캔하는 순회 방법(전위 순회, 중위 순회, 후위 순회)에 대해서도 알아보자.
이진 트리(Binary Tree, BT)
이진 트리는 모든 부모 노드가 왼쪽 자식과 오른쪽 자식만을 갖는 트리 구조이다.
만약 두 자식 중 하나만 있거나 둘 다 없는 노드가 존재해도 상관없다.


이진 트리에는 여러가지 하위 유형이 있다.
| 이진 트리 유형 | 내용 |
| 정 이진 트리 (Full Binary Tree) |
모든 노드가 0개 또는 2개의 자식 노드를 가진다. |
| 완전 이진 트리 (Complete Binary Tree) |
모든 레벨이 꽉 차 있고, 마지막 레벨은 왼쪽부터 연속적으로 노드가 채워짐 |
| 힙 (Heap) | 완전 이진 트리의 특별한 형태이다. 각 노드의 값이 자식 노드의 값보다 크거나 같은 경우 최대 힙, 작거나 같은 경우 최소 힙. |
| 균형 이진 트리 (Balanced Binary Tree) |
모든 노드에 대해 왼쪽 서브 트리와 오른쪽 서브 트리의 높이 차이가 1 이하 |
| 이진 탐색 트리 (Binary Search Tree, BST) |
노드의 왼쪽 서브 트리에는 해당 노드의 값보다 작은 값들만, 오른쪽 서브 트리에는 해당 노드의 값보다 큰 값들만 저장 |
| 포화 이진 트리 (Perfect Binary Tree) |
모든 내부 노드가 두 개의 자식 노드를 가지고 있고, 모든 리프 노드가 동일한 깊이 또는 레벨에 있음 |
| 편향 이진 트리 (Skewed Binary Tree) |
모든 노드가 오직 한 쪽 서브 트리만을 가짐 (왼쪽 또는 오른쪽) |
여기서 우선 완전 이진 트리에 대해서 알아보자.
완전 이진 트리 (Complete Binary Tree)
완전 이진 트리의 조건은 다음과 같다.
- 마지막 레벨을 제외한 모든 레벨에 노드가 가득 차 있다.
- 마지막 레벨에 한해서 왼쪽 -> 오른쪽 순으로 노드를 채우되, 반드시 끝까지 채우지 않아도 된다.

BFS(너비 우선 탐색)를 사용하여 스캔하면서, 스캔하는 순서대로 각 노드에 0, 1, 2, ... 값을 주면 배열에 저장하는 인덱스와 값을 1대1로 정확히 대응시킬 수 있다.
위 조건에 따르면, 높이가 k인 완전 이진 트리가 가질 수 있는 노드의 수는 최대 2^(k+1)-1 개이다.
이를 역산하면, n개의 노드를 저장할 수 있는 완전 이진 트리의 높이는 log n이다.
트리 순회 (Tree Traversal)
트리는 형제 노드의 순서 관계가 있는지를 기준으로 나누면 두 종류로 나눌 수 있다.
- 순서 트리(Ordered tree): 형제 노드의 순서 관계가 있음
- 무순서 트리(Unordered tree): 형제 노드의 순서 관계가 없음
이 중에서 순서 트리의 노드를 탐색하는 방법은 크게 두 가지이다:
- DFS(깊이 우선 탐색): 그래프 or 트리를 탐색할 때, 현재 노드의 자식들을 먼저 완전히 탐색
- BFS(너비 우선 탐색): 그래프 or 트리를 탐색할 때, 현재 노드의 모든 이웃 노드를 먼저 탐색한 후, 그 다음 레벨의 노드들을 탐색
그 중에서도 DFS를 활용한 탐색 방법은 다시 세 가지로 나뉜다.
1) 전위 순회(Preorder Traversal), 2) 중위 순회(Inorder Traversal), 3) 후위 순회(Postorder Traversal)
이 세 가지 방법은 특히 이진 트리에서 주로 사용된다.
| 순회 방식 | 설명 |
| 전위 순회 (Preorder) |
[현재 -> 왼쪽 -> 오른쪽] 1. 현재 노드를 먼저 방문 2. 왼쪽 서브트리를 전위 순회 3. 오른쪽 서브트리를 전위 순회 |
| 중위 순회 (Inorder) |
[왼쪽 -> 현재 -> 오른쪽] 1. 왼쪽 서브트리를 중위 순회 2. 현재 노드를 방문 3. 오른쪽 서브트리를 중위 순회 (이진 탐색 트리에서 중위 순회를 사용하면 오름차순으로 노드 값을 얻을 수 있음) |
| 후위 순회 (Postorder) |
[왼쪽 -> 오른쪽 -> 현재] 1. 왼쪽 서브트리를 후위 순회 2. 오른쪽 서브트리를 후위 순회 3. 현재 노드를 방문 |
위 테이블의 설명을 보면 알겠지만, 전위 - 중위 - 후위라는 각 명칭은 '현재 노드를 어떤 순서로 방문하는가'에 따라 붙여졌다.
그 외에는 언제나 왼쪽 서브트리 -> 오른쪽 서브트리 순서로 순회한다.
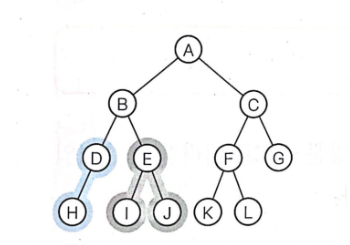
위 그림에서 각 순회방법이 어떤 경로로 진행되는지 체크해보자.
- 전위 순회: A B D H E I J C F K L G
- 중위 순회: H D B I E J A K F L C G
- 후위 순회: H D I J E B K L F G C A
코드를 통한 이해
백준 1991번 문제(트리 순회)를 통해 각 방식을 코드 수준에서 이해해볼 수 있다. (https://www.acmicpc.net/problem/1991)
# 문제: 트리 순회 (실버 1)
# 전위 순회
def preorder(node):
if node != '.':
left_node, right_node = BT[node][0], BT[node][1]
print(node, end='') # 해당 노드 스캔
preorder(left_node) # 왼쪽 서브트리 스캔
preorder(right_node) # 오른쪽 서브트리 스캔
# 중위 순회
def inorder(node):
if node != '.':
left_node, right_node = BT[node][0], BT[node][1]
inorder(left_node) # 왼쪽 서브트리 스캔
print(node, end='') # 해당 노드 스캔
inorder(right_node) # 오른쪽 서브트리 스캔
# 후위 순회
def postorder(node):
if node != '.':
left_node, right_node = BT[node][0], BT[node][1]
postorder(left_node) # 왼쪽 서브트리 스캔
postorder(right_node) # 오른쪽 서브트리 스캔
print(node, end='') # 해당 노드 스캔
### 입력 부분 ###
# 트리를 딕셔너리로 구현
BT = {}
for i in range(int(input())):
parent, left_node, right_node = map(str,input().split())
BT[parent] = [left_node, right_node]
### 출력 부분 ###
preorder('A')
print()
inorder('A')
print()
postorder('A')
재귀 함수로 구현했기 때문에, 수월하게 각 순회 방식의 로직을 파악할 수 있다.
'Computer Science > 자료구조 (Data Structure)' 카테고리의 다른 글
| 자료구조 | 그래프 기초(Graph) (1) | 2023.10.21 |
|---|---|
| 자료구조 | 이진 탐색 트리(Binary Search Tree, BST) (0) | 2023.10.20 |
| 자료구조 | 트리(Tree) (1) | 2023.10.20 |
| 자료구조 | 해시 테이블(Hash Table) (1) | 2023.10.19 |
| 자료구조 | 이중 연결 리스트, 원형 연결 리스트 (0) | 2023.10.17 |



