고정 헤더 영역
상세 컨텐츠
본문
그래프를 사용하는 이유
현실의 객체들은 언제나 다른 객체와의 연관성을 갖는다. 예를 들면, 사람과 사람은 혈연 학연 지연 등 다양한 기준으로 서로의 관계를 나타낼 수 있고, 도시와 도시는 위치와 거리를 기준으로 연결할 수 있다. 이처럼 그래프는 객체들 간의 이진 관계를 모델링하는데 사용되는 구조이다.
[이진 관계 (Binary Relations)]
두 개의 요소 사이에 성립하는 관계. 집합 A와 집합 B에 대해, 이진 관계는 A의 요소와 B의 요소 사이에 존재하는 관계를 나타낸다. 이 관계는 주로 집합 A *B의 부분집합으로 표현되며, 이 부분집합의 각 원소는 순서쌍 (a,b)로 나타낼 수 있다.
예를 들어, 집합 A = {1,2,3}와 집합 B = {a,b}가 있다고 하면, 이진 관계의 예는 다음과 같다: {(1, a), (2, a) ... (2, b), (3, b)}
현실을 매우 효과적으로 표현할 수 있는 특성 덕분에 그래프는 다양하게 응용된다. 예를 들면 도로 네트워크, SNS, 전력 그리드 등에서 그래프 이론이 사용된다. 앞에서 배운 트리도 그래프의 하위집합이다.
그래프 정의
"그래프를 정의해보세요."

가장 일반적인 의미에서 그래프(graph)를 정의하면, 그래프는 순서쌍 G = (V, E)으로 정의할 수 있다.
즉, Vertex(정점)와 이들을 연결하는 Edge(간선)의 집합으로 구성된 자료구조이다.
위 정의를 그대로 따르는 형태의 그래프는 방향성이 없는(무향) 간단한 그래프이다.
- 간선에 방향성이 부여되면 방향 그래프(Directed Graph) 또는 디그래프(Digraph)라고 부른다.
- 간선에 가중치나 비용이 할당되면 가중 그래프(Weighted Graph)라고 부른다.
- 간선에 방향성과 가중치가 함께 부여되면 가중치 방향 그래프(Weighted Directed Graph)라고 부른다.
그래프 기본 구조
1. 정점과 간선의 상태만 같다면, 같은 그래프로 취급한다.

이 그림에서 A 케이스와 B 케이스는 서로 같은 그래프이다.
2. 연결요소(Connected Component)
하나의 그래프는 여러개의 연결요소(Connected Component)로 이루어질 수 있다.
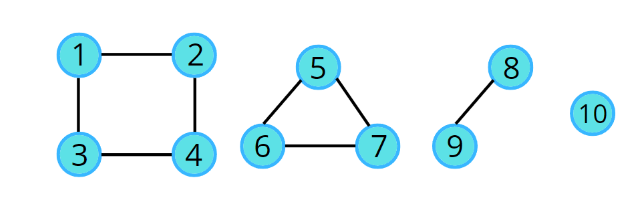
위 구조는 하나의 그래프라고 볼 수 있을까?
답은 Yes. 이 전체(정점과 간선의 모든 집합체)를 하나의 그래프로 정의했다면
이 그래프는 싱글 노드인 (10)까지 포함해서 총 4개의 연결요소로 이루어진 비연결 그래프라고도 볼 수 있다.
(In this case, we can say, the graph has been broken down into 4 different connected components.)
정점이 10개, 간선이 8개인 그래프이다.
3. 부분 그래프(Subgraph)

말 그대로 특정 그래프의 정점과 간선으로 이루어진 하위집합 그래프이다.
가운데, 오른쪽 그래프는 각각 왼쪽 그래프의 부분 그래프 예시이다.
주요 용어, 개념
| 용어 | 설명 |
| Vertex, Node | 정점 |
| Edge, Link | 연결선(간선) |
| Arc | 방향이 있는 간선 |
| Path | 정점 x → 정점 y에 이르는 루트에 있는(간선으로 연결된) 정점들의 순서 집합. - 특수한 조건이 걸려있지 않다면 방문한 정점을 재방문할 수도 있다. |
| Simple Path | 중복된 정점이 없는 경로 |
| Cycle | 시작 정점과 종료 정점이 동일한 경로 |
| Loop | 시작과 끝이 같은 단일 간선 |
| Adjacent (인접) | 두 정점이 간선으로 직접 연결되어 있을 때 |
| Degree (차수) | 그래프 내의 특정 정점에 연결된 간선의 수 방향 그래프일 경우: - 입력 차수(in-degree): 한 꼭짓점으로 들어오는 변의 개수 - 출력 차수(out-degree): 한 꼭짓점에서 나가는 변의 개수 |
그래프 종류
그래프는 워낙 특성이 다양하기 때문에, 특성에 따른 분류도 여러가지가 있다.
밀집도에 따른 분류
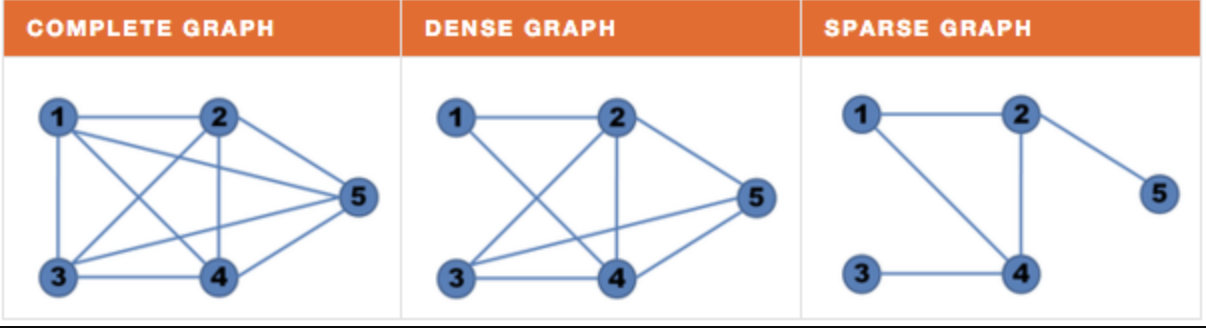
| 그래프 | 설명 |
| 완전 그래프 (Complete Graph) | 모든 정점이 서로 직접 연결된 그래프. |
| 밀집 그래프 (Dense Graph) | 가능한 최대 간선 수에 근접한 수의 간선을 가진 그래프. 정확한 기준은 없는 듯. Introductions to Algorithms에 따르면, |E| 값이 |V|^2에 가까울수록 밀집 |
| 희소 그래프 (Sparse Graph) | 가능한 최대 간선 수에 비해 적은 수의 간선을 가진 그래프. Introductions to Algorithms에 따르면, |E| 값이 |V|^2보다 현저히 작은 경우 |
방향성 및 가중치에 따른 분류
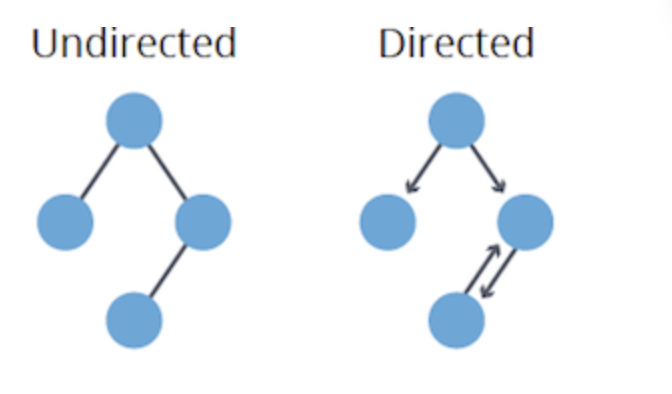
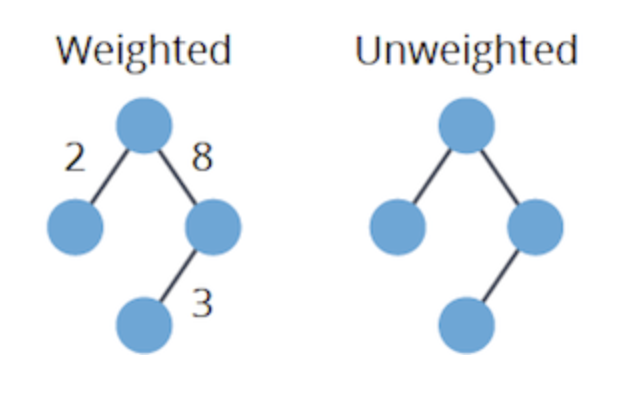
| 그래프 | 설명 |
| 방향 그래프 (Directed Graph or Digraph) | 간선에 방향성이 있는 그래프. |
| 무방향 그래프 (Undirected Graph) | 간선에 방향성이 없는 그래프. |
| 가중 그래프 (Weighted Graph) | 간선에 가중치가 할당된 그래프. |
| 비가중 그래프 (Unweighted Graph) | 모든 간선의 가중치가 동일한 그래프. (= 가중치가 없는 것과 마찬가지) |
연결성에 따른 분류
| 그래프 | 설명 |
| 연결 그래프 (Connected Graph) | 모든 정점 사이에 경로가 있는 그래프. (모든 정점 사이에 간선이 있는 게 아님. 완전 그래프와 헷갈리지 않도록 유의) |
| 비연결 그래프 (Disconnected Graph) | 일부 정점 사이에 경로가 없는 그래프. |
| 이중 연결 그래프 (Biconnected Graph) | 어떤 두 정점 사이의 경로가 최소 두 개 이상인 그래프. |
기타 분류
| 그래프 | 설명 |
| 사이클이 없는 그래프 (Acyclic Graph) | 사이클을 포함하지 않는 그래프. |
| 트리 (Tree) | 사이클이 없고, 모든 정점이 연결된 그래프. |
| 신장 트리 (Spanning Tree) | 그래프의 모든 정점을 포함하면서 트리의 속성을 만족하는 부분 그래프. |
그래프 표현법
위에서 쭉 봤듯이, 그래프를 시각적으로 표현하는 것은 우리에게 익숙하고 직관적이다.
그러나 이를 컴퓨터에 인식시키는 것은 다른 문제이다.
그래프를 컴퓨터 메모리에 저장하고 표현하기 위해 주로 사용되는 두 가지 주요 방법은 1) 인접 리스트법, 2) 인접 행렬법이다.
인접 리스트법 (Adjacency List)
인접 리스트법은 각 정점에 연결된 다른 정점들의 목록을 저장하는 방식으로 그래프를 표현한다. 주로 선호되는 방법이라고 한다.
파이썬에서는 딕셔너리 형태를 주로 사용한다.
장점:
- 메모리 공간을 O(V+E)만 필요로 한다. (V = 정점의 수, E = 간선의 수)
- 낮은 밀도의 희소 그래프에서 더욱 메모리 효율적이다.
단점:
- 두 정점 간의 연결 여부를 확인하는 데 인접 행렬법 대비 시간이 더 걸릴 수 있다.
인접 리스트법 구현
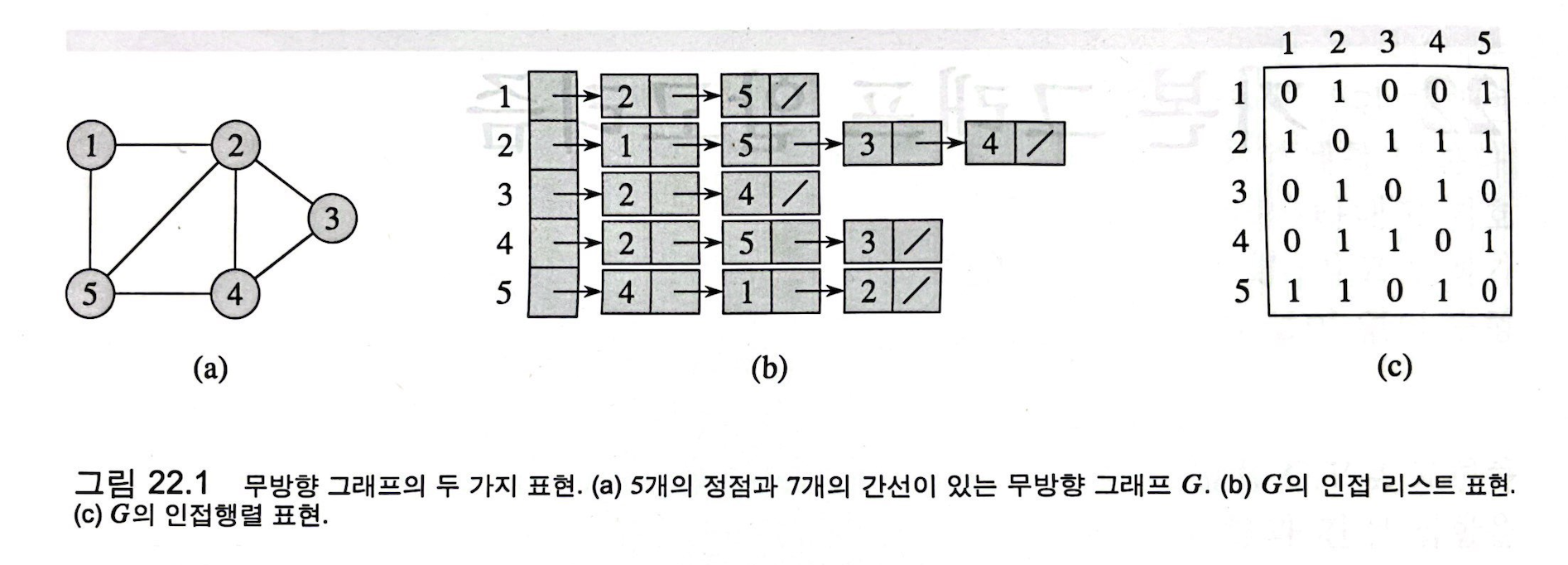
- 무방향 그래프에서는 두 정점 x, y가 연결되어 있다면 x의 인덱스에 y를 포함하고, y의 인덱스에도 x를 포함해준다.
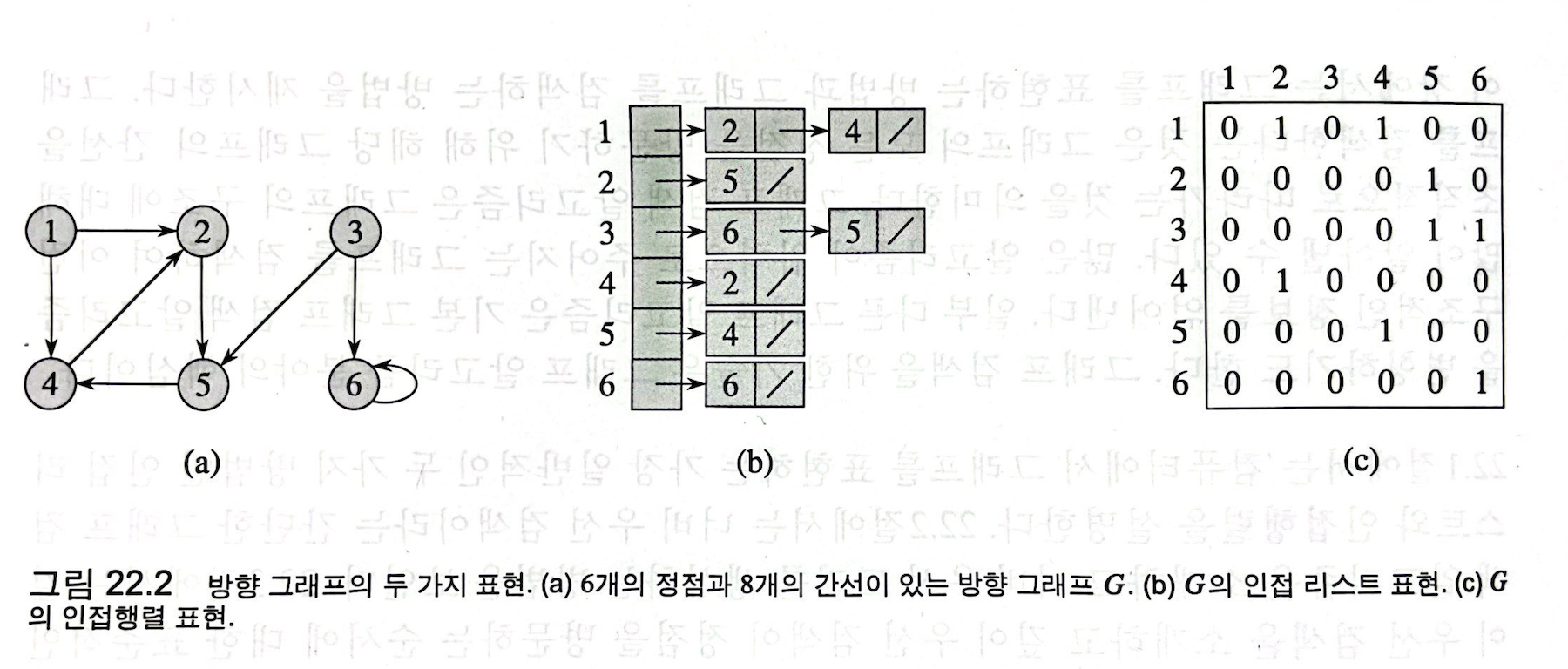
- 방향 그래프에서는 두 정점 x, y가 x -> y 방향으로 연결되어 있다면, x의 인덱스에만 y를 포함해준다. 즉, 각 인덱스마다 해당 정점에서 출발하는 간선이 어떤 정점을 가리키고 있는지만 표시하면 된다.
위 이미지를 기반으로 코드를 구현하면 다음과 같다.
# 인접 리스트법을 통한 무방향 그래프 표현 (그림 22.1)
graph = {1: [2, 5],
2: [1, 5, 3, 4],
3: [2, 4],
4: [2, 5, 3],
5: [4, 1, 2]}
# 인접 리스트법을 통한 방향 그래프 표현 (그림 22.2)
graph = {1: [2, 4],
2: [5],
3: [5, 6],
4: [2],
5: [4],
6: [6]}
인접 행렬법
인접 행렬법은 그래프의 정점들을 행과 열로 나타내는 2차원 배열로 그래프를 표현한다.
인접 행렬법의 경우에도 마찬가지의 원칙이 적용된다. 그 결과, 무방향 그래프일 경우 인접 행렬법으로 표현한 행렬은 대각선을 기준으로 대칭이 된다.
- 장점:
- 두 정점 간의 연결 여부를 O(1)의 시간 복잡도로 확인할 수 있다.
- 구현이 직관적이고 간단하다.
- 단점:
- 메모리 공간을 O(V^2)만큼 필요로 한다 (V = 정점의 수).
- 희소 그래프에서는 메모리 낭비가 심각할 수 있다.
인접 행렬법은 높은 밀도 그래프, 주어진 두 정점을 연결하는 간선이 있는지를 빠르게 확인할 필요가 있을 때 더 효율적이다.
# 인접 행렬법을 통한 무방향 그래프 표현 (그림 22.1)
graph = [[0, 1, 0, 0, 1],
[1, 0, 1, 1, 1],
[0, 1, 0, 1, 0],
[0, 1, 1, 0, 1],
[1, 1, 0, 1, 0]] # 대각선을 기준으로 대칭임을 확인 가능
# 인접 행렬법을 통한 방향 그래프 표현 (그림 22.2)
graph = [[0, 1, 0, 1, 1, 0],
[0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 1, 1],
[0, 1, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0],
[0, 0, 0, 0, 0, 1]] # 인접 리스트법 대비 메모리 공간이 낭비되는 경향이 있다.
'Computer Science > 자료구조 (Data Structure)' 카테고리의 다른 글
| 자료구조 | 유니온-파인드(Union-Find) (1) | 2023.10.23 |
|---|---|
| 자료구조 | 신장 트리(ST), 최소 신장 트리(MST) (1) | 2023.10.22 |
| 자료구조 | 이진 탐색 트리(Binary Search Tree, BST) (0) | 2023.10.20 |
| 자료구조 | 이진 트리, 트리 순회(Tree Traversal) (0) | 2023.10.20 |
| 자료구조 | 트리(Tree) (1) | 2023.10.20 |




